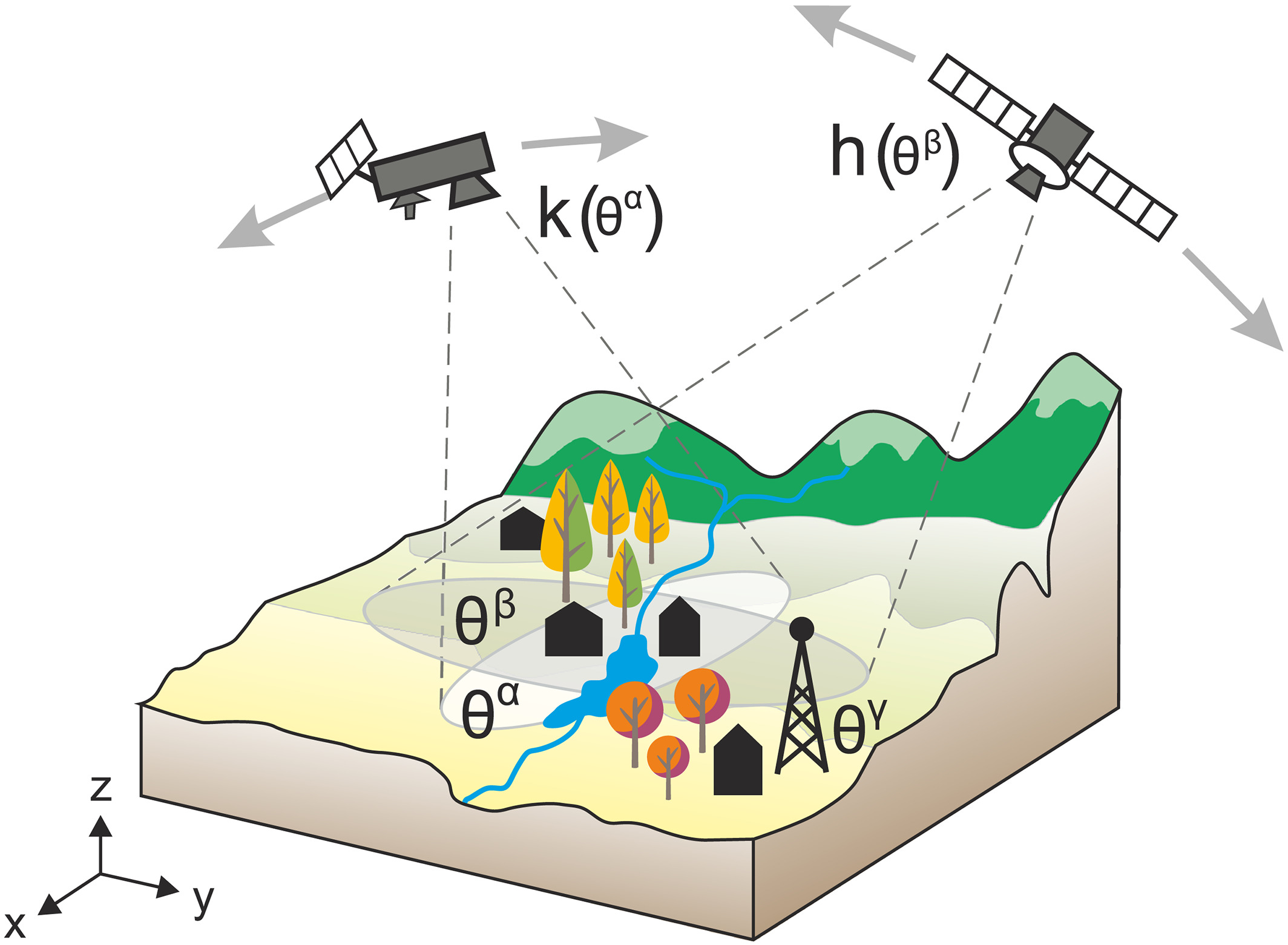
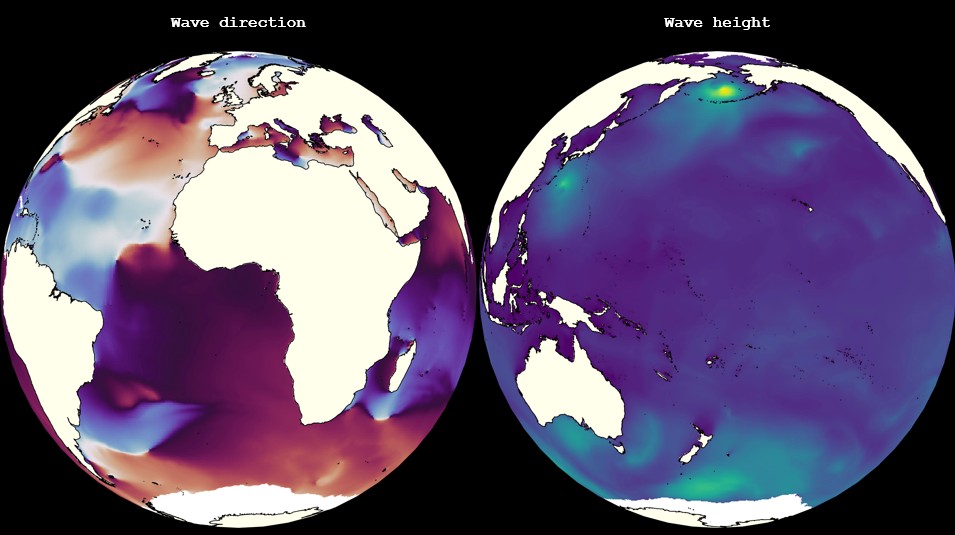
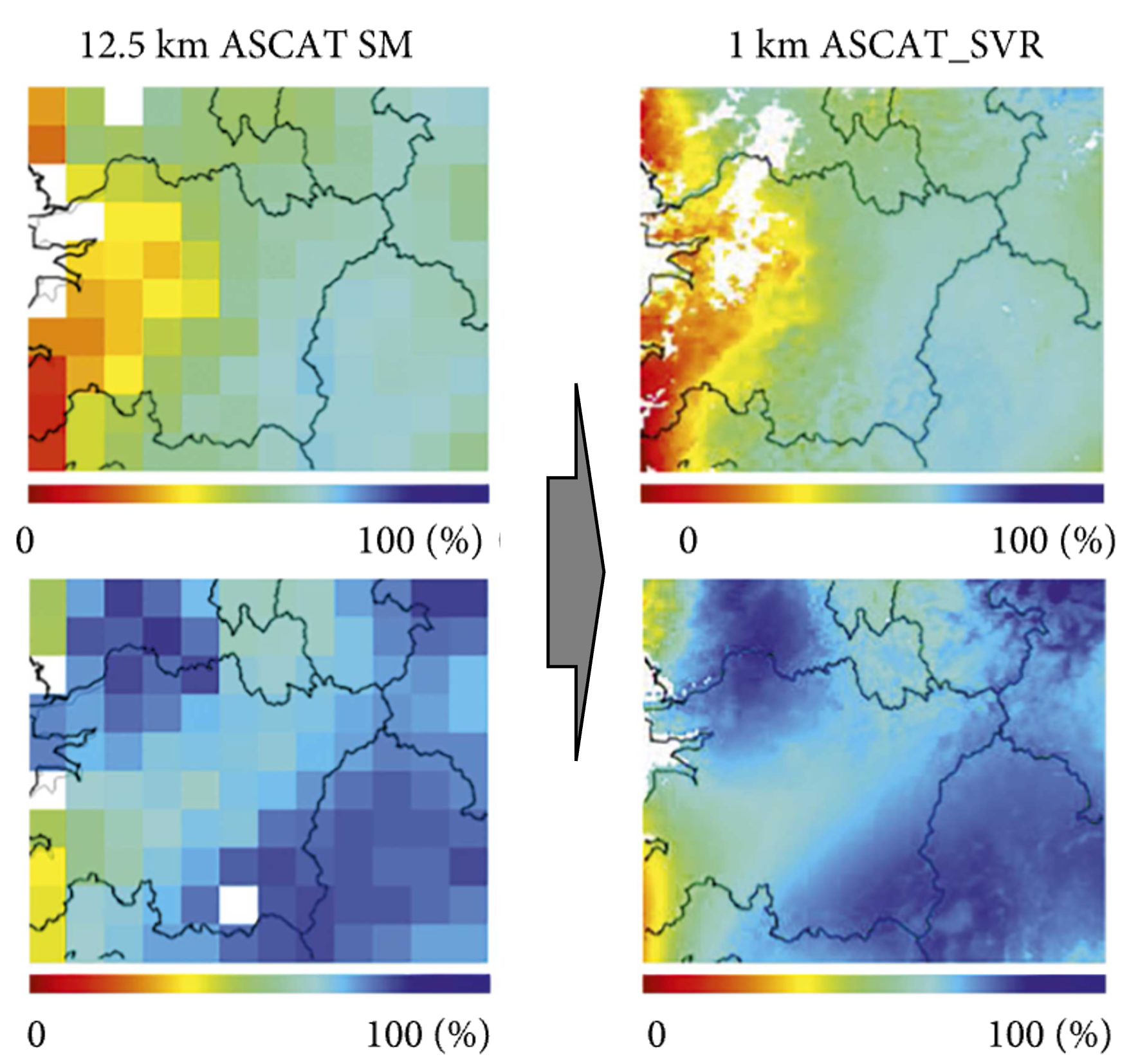
Water balance budgeting is crucial in Earth science for maintaining ecosystems, supporting agriculture, and managing water resources.
The water balance equation in Earth science, P = E + R + etc., represents the interactions between precipitation (P), evaporation (E), runoff (R), etc. (e.g., soil moisture, water in vegetation, ground water) within a specific region. Bayesian inference can be employed to solve this equation by using prior knowledge to create probability distributions for the variables involved. As new data is gathered, these probability distributions are updated, enabling more accurate predictions and better water resource management.

What we aim to achieve
We aim to achieve several goals by solving the water balance equation using Bayesian inference:
- Improved predictions: Bayesian inference allows for better estimation of the variables involved in the water balance equation by incorporating prior knowledge and updating probability distributions with new data.
- Uncertainty quantification: Researchers can assess the uncertainty associated with the estimates, enabling more informed decision-making and risk assessment in water resource management.
- Adaptive management: Bayesian inference offers a flexible and adaptive approach to managing water resources by updating the model as new information becomes available, leading to continuous improvement in predictions and decision-making.
- Enhanced understanding: The application of Bayesian inference to the water balance equation can lead to a deeper understanding of hydrological processes, helping researchers better comprehend the complex interactions between precipitation, evaporation, and runoff.
Data and analytic skills we use for this project
To effectively solve the water balance equation using Bayesian inference, we need following analytic skills:
- Statistical Background: A solid foundation in statistics, especially in probability theory and Bayesian statistics, is essential for understanding the principles behind Bayesian inference and applying them to the water balance equation.
- Programming Skills: Proficiency in programming languages such as R, Python, or MATLAB is necessary for data analysis, manipulation, and visualization, as well as implementing Bayesian inference algorithms. (e.g., PyMC4)
- Domain Knowledge: A strong understanding of Earth science and hydrology is required to comprehend the underlying processes and factors influencing the water balance equation, ensuring that the Bayesian inference model is built on a sound scientific basis.
- Model Development and Evaluation: Researchers need the ability to develop and evaluate different Bayesian inference models, including selecting appropriate priors, likelihood functions, and updating schemes, as well as assessing model performance using metrics.
- Uncertainty Analysis: Skills in uncertainty analysis are essential to quantify the uncertainties associated with the estimates generated by the Bayesian inference model and to make informed decisions based on the results.
Our supportive academic environment is here to help you learn and develop the necessary skills along the way.
This project aims not only to investigate the water balance with the Bayesian machine learning approach but also to explore other related research topics below. If you are interested in any of the following research areas, please do not hesitate to contact me!
- Impact of Climate Change: Investigate the influence of climate change on water balance components (precipitation, evaporation, and runoff) and develop adaptive management strategies to mitigate potential impacts on water resources.
- Machine Learning for Water Balance: Apply advanced machine learning techniques, such as deep learning or reinforcement learning, to improve predictions and optimize water balance management strategies.
- Remote Sensing for Water Balance Estimation: Utilize remote sensing data from satellites, drones, or ground-based sensors to estimate water balance components and improve the spatial and temporal resolution of hydrological models.
- Urban Water Balance: Study the effects of urbanization on the water balance, including changes in land use, impervious surfaces, and green infrastructure, and propose strategies to enhance urban water management.
- Snowmelt and Water Balance: Analyze the role of snowmelt in the water balance of mountainous regions, and develop methods to better incorporate snowmelt dynamics into water balance models.
- Groundwater Recharge Estimation: Develop novel approaches to estimate groundwater recharge rates, a key component of the water balance, and investigate the implications of recharge variability on water resources management.
- Water Balance and Agricultural Productivity: Examine the relationships between water balance components, irrigation efficiency, and crop yield, and develop strategies to optimize water use in agriculture while minimizing environmental impacts.
- Real-time Water Balance Monitoring: Develop an integrated monitoring system that combines sensors, remote sensing data, and hydrological models to provide real-time information on water balance components for improved decision-making.
- Socioeconomic Impacts of Water Balance Changes: Investigate the socioeconomic consequences of changes in water balance, such as the effects on water availability, food security, public health, and migration, and propose policy recommendations to address these challenges.